Y a-t-il, vraiment, deux flux de rayonnement parvenant au sol dea Terre ?

Le « bilan thermique de la terre » est déjà présenté ailleurs sur ce site et rappelé ici (source : https://actugeologique.fr/2022/07/le-bilan-radiatif-de-la-terre/)

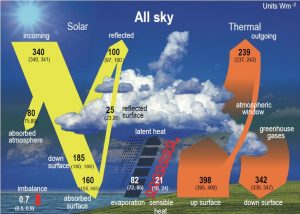
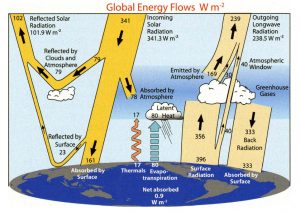
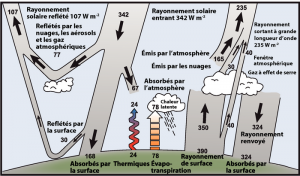
Ces bilans montrent que l’on égale l’énergie entrante au sol avec l’énergie sortante du sol.
Comme le sol est en équilibre thermique, au sens où sa température moyenne au cours des siècles reste aux alentours de 15°C, l’égalité entre l’énergie entrante et l’énergie sortante est donc logique et nous ne contestons pas ce point.

Par contre les totaux obtenus sont quand à eux tout à fait contestables pour deux raisons au
moins, que nous détaillons ici. Nous prenons les chiffres du troisième schéma, intitulé Earth’s energy global budget, K. Trenberth et al., American Meteorological Society, 2009. et utilisés par le GIEC.

– La première raison est que les deux totaux valent 492 W/m². Or, un corps qui recevrait 492 W/m² serait à une température égale à la racine quatrième de 492.10⁸/5.67 soit environ 32°C. Pourtant le sol est à 15°C de moyenne. Comment explique-t-on ceci ?

En fait le total de l’énergie sortante s’obtient en faisant une somme de trois énergies :

a) 390 W/m², puissance d’un rayonnement infrarouge correspondant à un corps noir à la température de 15°C. Cela signifie bien que le sol est assimilé à un corps noir, puisque l’émissivité a été prise égale à 1.

b) 78 W/m² correspondant à l’évapo-transpiration du sol.

c) 24 W/m² correspondant à la convection (notée thermique sur le schéma)

On en déduit ensuite que le total de l’énergie entrante doit être « en moyenne » calculée en ajoutant deux types de rayonnement entrant :

1) Le rayonnement en provenance du soleil, évalué au sol à 168 W/m², après la division par 4 qui est faite de la constante solaire, après déduction de l’albédo (107 sur le schéma) et après déduction de l’énergie absorbée par l’atmosphère (67 sur le schéma).

2) Le rayonnement en provenance des gaz à effet de serre, calculé par différence. La valeur obtenue par cette méthode est de 324 W/m² sur le schéma. Elle est considérée comme exacte parce que les instruments de mesure perçoivent un rayonnement venant du haut ayant à peu près cette valeur. Personne ne se demande si ce rayonnement vient d’autre chose que des gaz à effet de serre. Nous pensons, nous, qu’affirmer qu’il y a d’un côté un rayonnement solaire à 340 W/m² et de l’autre un rayonnement IR quasiment égal (en W/m²) à celui du soleil venant des gaz à effet de serre et valant 324 W/m² est de l’ordre du déraisonnable et donc en dehors de la science.

On obtient ainsi la « belle » égalité 390 + 78 + 24 = 168 + 324 = 490

Cette « belle » égalité prouverait l’existence d’un effet de serre…

Nous affirmons ici que ce n’est pas vrai. Cette égalité est tout simplement fausse et nous allons expliquer pourquoi ci-dessous. Auparavant, il convient de lire la définition et les propriétés d’un corps noir.

En voici une : « Un corps noir en équilibre thermique (qui est à une température constante) émet un rayonnement électromagnétique appelé rayonnement du corps noir. Le rayonnement est émis selon la loi de Planck, ce qui signifie qu’il a un spectre qui est déterminé par la température seule, et non par la forme ou la composition du corps. »

Les irradiances sortantes ont donc été additionnées, sans tenir compte qu’un corps noir idéal, qui rayonne bien à sa température, donc considéré ici comme étant à 15°C, ne perd en aucun cas d’énergie en plus par évapotranspiration ou par convection. Un corps noir ne peut avoir d’échange de chaleur avec son environnement que par rayonnement. Ici, il en a par d’autres formes d’échanges de chaleur. Ceci est une première contradiction.

La seconde raison achève de démolir ce schéma. Le sol est à 15°C et pas à 32°C. L’irradiance qu’il reçoit doit donc être de 390 W/m² environ, au maximum, et non pas de 490 W/m². Par ailleurs, a-t-on le droit d’ajouter des irradiances pour trouver une température ? En additionnant les irradiances, on empile (plutôt qu’on ajoute) aussi les températures qui vont avec, même si la formule reliant les températures à la puissance n’est pas linéaire . De plus, un rayonnement qui atteint une surface qui est déjà à une température supérieure à celle qui est associée au rayonnement incident ne chauffera pas cette surface. Ce schéma suggère le contraire. Prenons la Terre à un endroit donné, le matin avant le lever du soleil. La température au sol est déjà en moyenne de plus de 15°C. Admettons qu’en fin de nuit, elle ait baissé. Toutes les mesures montrent que la baisse des températures à la surface de l’océan n’est que de 1°C environ et sur les terres immergées de 10°C à 20°C.

Supposons donc cette surface à 0°C pour simplifier. Cet endroit reçoit selon ce schéma 168 W/m² « en moyenne », une puissance de rayonnement qui est associée à la température de -31°C environ, donc bien plus « froide » que la température au sol. Comment un tel rayonnement pourrait-il faire s’évaporer de l’eau ?… et tout simplement comment pourrait-il chauffer tout court une terre à 0°C ? Cela n’a pas de sens.

Tout ceci montre à l’évidence qu’il n’est tout simplement pas pertinent de raisonner sur des moyennes d’irradiances et encore moins pertinent d’additionner des moyennes d’irradiances. La raison en est que la formule de Stefan-Boltzmann s’applique de façon ponctuelle et instantanée. L’appliquer à des moyennes sur des surfaces ou à des moyennes sur la journée est dépourvu de sens physique. Comme le dénoncent déjà Gerlich et Tscheuschner en 2009, tout ces calculs sont dénués de sens physique et en conséquence sont en dehors de la science.

Reprenons le problème plus simplement :

Y a-t-il, vraiment, deux flux de rayonnement parvenant au sol de la Terre ?

Y a-t-il vraiment DEUX flux d’énergie radiative parvenant au sol ?
Le bilan radiatif proposé par le GIEC comporte deux flux, l’un en provenance du soleil et l’autre en provenance de l’Atmosphère, soit, compte tenu des propriétés des gaz contenus dans l’Atmosphère, en provenance des gaz à effet de serre.

Le second flux en effet ne peut pas provenir de gaz inertes aux rayonnements, comme le sont l’azote et l’oxygène. Il ne peut que provenir de gaz dits à effet de serre, c’est-à-dire ayant la capacité d’absorber des rayonnements.

Il s’agit là d’un point crucial, puisque c’est l’un des fondements de l’introduction par les scientifiques d’un effet de serre.

Nous analysons ici ce qu’il en est, à notre point de vue.

a) Remarque préalable n°1 :

Le bilan radiatif proposé contrevient à une règle pratique physique concernant les bilans radiatifs, qui est la suivante : afin de montrer qu’un objet donné est en équilibre radiatif, il convient de faire un bilan radiatif qui soit instantané. Le bilan radiatif qui est fait est une « sorte de bilan » peu orthodoxe en ce qu’il porte sur une durée de 24 h. Un bilan radiatif illustrant l’équilibre doit montrer au contraire qu’à chaque instant l’objet étudié perd autant d’énergie qu’il en reçoit.

Selon nous le système Terre-Atmosphère est en équilibre radiatif parce qu’à chaque instant effectivement, ce système reçoit autant d’énergie qu’il en perd. Il y a un côté nuit qui équilibre à chaque instant ce qui entre du côté jour, diminué de ce qui sort côté jour. Cet équilibre se traduit par une température moyenne, à peu près constante, du système depuis des siècles, située autour de
-18°C.

Au sol, la température moyenne de l’hémisphère qui est éclairé reste constante quand la Terre tourne, bien que ce ne soit pas toujours le même hémisphère qui soit éclairé. De même la température de l’hémisphère qui est dans la nuit reste constante quand la Terre tourne. L’intérêt de faire un bilan radiatif sur 24 h non seulement nous échappe, mais conduit à notre avis à des conclusions erronées.

Le sol n’est pas pour sa part en équilibre radiatif. Il est en équilibre thermique, ce qui n’est pas la même chose. En plus des radiations, plusieurs phénomènes non radiatifs sont à prendre en compte pour expliquer cet équilibre thermique, sans en oublier aucun.
Or, deux phénomènes très importants sont passés sous silence : l’inertie thermique des océans et le gradient thermique dû au poids de l’Atmosphère.

b) Remarque préalable n°2 :

Une étrangeté scientifique figure à notre avis dans le bilan radiatif qui est présenté. Il est illustré par la phrase souvent employée suivante :

« Tout se passe (sur Terre) comme si chaque point de la surface Terrestre recevait au sol un rayonnement en provenance du soleil de 163,3 W/m² ».

Vous pouvez voir le chiffre de 163,3 W/m² sur le schéma de la NASA en PJ.

Vous pouvez voir aussi ce que nous appelons une étrangeté scientifique, à savoir le chiffre avancé de 340,4 W/m² figurant quand à lui comme étant la puissance du rayonnement solaire arrivant en haut de l’Atmosphère.
Il est considéré par conséquent que le soleil agit comme si nous étions entouré dans toutes les directions par un feu céleste de 340,4 W/m² venant de tous les points de la sphère céleste.
Cette approximation vient de deux éléments qui sont à notre avis mal interprétés.

– Le premier élément est que la Terre tourne. Il en résulterait cette uniformité du rayonnement solaire entrant.

– Le second élément est que l’objet qui réceptionne ce rayonnement est entouré de fluides, à savoir des océans et de l’Atmosphère. Cet élément, qui est inexact sur la Lune, confirmerait l’uniformité du rayonnement solaire entrant.

Nous affirmons que l’approximation qui est ainsi faite n’est pas acceptable sur le plan scientifique.
Pourquoi ?

La première raison résulte des mesures réelles des températures au sol : elles varient certes de façon moins considérable que sur la Lune, mais sont extrêmement éloignées d’une situation où elles seraient uniformes : elles varient de -70°C environ à 50°C environ soit une amplitude de 120°C.

La seconde raison est que les calculs sont alors faits comme si la Terre n’était pas ronde, alors que la rotondité de la Terre conduit à l’existence de rayonnements rasants vers les pôles, n’ayant rien à voir avec les rayonnements vers l’équateur, lesquels parviennent perpendiculairement au sol.

La troisième raison est une confusion entre le rayonnement et la chaleur.
En effet les rayonnements en provenance du soleil ne sont nullement répartis sur toute la surface de la Terre, mais ne parviennent que sur un hémisphère éclairé, soit la moitié de la surface Terrestre.
Par contre la chaleur est répartie un peu partout en raison des phénomènes de circulation océanique et atmosphérique.
Mais ce n’est parce que la chaleur est ainsi répartie que nous sommes en droit d’admettre qu’il en est de même du rayonnement solaire. Ceci est à notre avis une faute scientifique grave. A notre connaissance, les propriétés des fluides que sont l’océan et l’Atmosphère ne se téléportent pas en haut de l’Atmosphère comme le suggère la prise en compte de cette étrangeté scientifique que constitue le chiffre indiqué de 340,4 W/m² à l’entrée dans l’Atmosphère.

Il en résulte que cette approximation n’est pas acceptable. Dans la réalité, le jour, l’irradiance entrante en haut de l’Atmosphère est variable en fonction de θ et vaut 1361 cosθ. La nuit l’irradiance est nulle. Cela n’a rien à voir avec un rayonnement entrant uniforme.

c) Analyse de l’existence supposée de deux flux :<

L’erreur faite ci-dessus conduit à inventer qu’il y aurait deux flux influençant la température au sol, l’un en provenance du soleil, d’intensité 163,3 W/m² et l’autre en provenance de l’Atmosphère et donc des gaz à effet de serre, d’une intensité évaluée à 340,3 W/m² .

On peut noter au passage que selon ce schéma, le flux solaire seul conduirait à une température de 231 K = – 41°C si l’on considérait vraiment cet éclairage comme égal en tout point.

Le flux venant des gaz à effet de serre donnerait seul une température de 278 K = 5°C.

Ces chiffres sont tout aussi extravagants à notre avis que le chiffre erroné de -129°C obtenu par Gerlich et Tscheuschner qui ont négligé les influences sur la température des phénomènes non radiatifs, et pour la même raison. Ces chiffres ne prennent en compte que les phénomènes radiatifs et ne sont donc pas plus crédibles que celui de Gerlich et Tscheuschner.
Ces deux flux sont ensuite additionnés.

Il y a derrière cette addition une très grosse question. La température est une quantité intensive, ce qui veut dire que les températures ne s’additionnent pas. Pour l’illustrer simplement, faisons l’expérience suivante : nous mélangeons dans un verre plus grand le contenu en eau de deux verres contenant la même quantité d’eau.
L’un contient de l’eau à la température de 15°C. L’autre également. Après le mélange, la quantité d’eau a doublé. Par contre la température est restée de 15°C. La quantité d’eau est une grandeur extensive que l’on peut et doit additionner. La température est une grandeur intensive que l’on ne peut pas et ne doit pas additionner. Or, additionner des irradiances cumule des températures. Si nous additionnons 163 ,3 W/m² et 340,3 W/m² , nous obtenons 503,6 W/m² qui donnerait une température de 307 K = 34°C.

Un tel calcul est-il légitime ?

Nous ne le croyons pas.
Pourquoi ?

Pour le voir il convient comme toujours de ne pas se référer à des moyennes globales mais à séparer ce qui se passe le jour de ce qui se passe la nuit. Les deux situations sont très différentes et à notre avis, ne pas les séparer ne peut que conduire à des impasses scientifiques.

La nuit il est clair qu’il n’existe pas deux flux. Le flux solaire est absent. Il ne reste que le flux de l’Atmosphère vers le sol, grâce effectivement à la présence de gaz à effet de serre. Grâce à eux, l’Atmosphère a pu emmagasiner de jour de la chaleur en provenance du rayonnement solaire et est en mesure de le restituer la nuit. Mais, la nuit, le sol refroidit et ne se réchauffe pas. Donc les gaz à effet de serre doivent avoir un rayonnement dont la puissance, la nuit, n’est pas suffisante pour pouvoir réchauffer le sol, puisqu’au contraire celui-ci refroidit.

Ceci est confirmé par la mesure des instruments AERI qui donnent la nuit, selon les sources, un rayonnement en provenance des gaz à effet de serre d’au plus 315 W/m² correspondant au plus à une température de 0°C environ. Un tel rayonnement ne peut pas chauffer le sol qui est déjà assez nettement au dessus de 0°C en moyenne. Bien entendu les chiffres varient selon la position des surfaces considérées. Mais par exemple aux pôles, les gaz à effet de serre n’émettent pas, loin de là, de rayonnement d’une puissance suffisante pour chauffer les pôles. C’est même l’inverse puisque plusieurs articles scientifiques font mention d’un « forçage négatif » du côté des pôles.
Qu’en est-il le jour ?
Il faut savoir qu’environ 50 % du rayonnement solaire se situe dans les petites longueurs d’onde, allant des rayons gamma et ultraviolet aux rayonnements de l’IR proche (non compris) en passant par le rayonnement visible. Ce rayonnement apparemment traverse l’Atmosphère sans encombre, déduction faite cependant de l’albédo.

Les autres 50 % représentent le rayonnement infrarouge proche venant du soleil, d’une puissance par conséquent de 1361/2 W/m² = 680,5 W/m².
Ce rayonnement, dans le bilan radiatif du GIEC, malgré sa puissance très notable (680W/m² , ce n’est pas rien) est soit inclus dans les 163,3, W/m² , soit absent des considérations qui sont faites.

Or, si l’on raisonne comme nous proposons de le faire, en séparant le jour et la nuit, nous avons en première approximation :
– 680W/m² de lumière à petite longueur d’onde qui parviennent en haut de l’Atmosphère côté jour.
– 680 W/m² de lumière dans l’infrarouge proche qui parviennent en haut de l’Atmosphère côté jour.

De ces chiffres, il faut déduite l’albédo de 30 % , de façon semble-t-il différente entre les types de lumière. Les nuages, la glace, la neige réfléchiraient 80 % de la lumière aux petites longueurs d’onde. Compte-tenu que ces trois éléments représentent 25 % de l’albédo, cela nous donne au total un peu moins que (1-0,25) x 680 = 510 W/m² , disons 490 W/m² de lumière à petite longueur d’onde parvenant en haut de l’Atmosphère et pénétrant dans celui-ci, le jour.

– Par contre, les 5 % restants sont de la lumière réfléchie se situant dans l’infrarouge proche, ce qui nous donne 0,7×1361 – 490= 463 W/m² de lumière dans l’infrarouge proche qui pénètrent aussi dans l’Atmosphère, le jour.

Il faut ensuite déduire l’absorption due à la traversée de cet Atmosphère. Il est admis que les rayonnements de petite longueur d’onde ne sont pas absorbés : l’Atmosphère est transparente à ce type de lumière. Les 25 % de ce qui pénètre dans l’Atmosphère et qui sont absorbés par lui représentent donc 115 W/m², situés dans l’infrarouge. Il reste 348 W/m² de lumière dans l’infrarouge qui parvient au sol et qui provient du soleil, toujours le jour.

Les chiffres indiqués seraient à vérifier par des mesures plus précises mais leur ordre de grandeur est significatif.

Le rayonnement infrarouge en particulier serait de l’ordre de 348 W/m² . Or le bilan du GIEC indique un rayonnement de l’Atmosphère vers le sol de 340 W/m² . Ces chiffres sont très comparables.

A notre avis, il s’agit donc de la partie du rayonnement solaire située dans l’infrarouge lointain qui, après avoir traversé l’Atmosphère et donc après avoir changé de longueur d’onde puisque réémis par l’eau liquide ou solide contenue dans l’Atmosphère ou encore par les gaz à effet de serre eux-mêmes, parvient jusqu’au sol.
Admettre qu’un rayonnement en plus, qu’un second flux venant de l’Atmosphère puisse s’ajouter à ce rayonnement solaire, c’est admettre que l’Atmosphère est par elle-même une source de chaleur et non un intermédiaire transmettant et transformant le rayonnement qu’elle reçoit.

C’est donc créer de l’énergie à partir de rien, ce qui est contraire aux lois de la physique.

Nous concluons pour notre part qu’il est erroné de considérer qu’il existe deux flux bien distincts parvenant au sol. C’est tout à fait clair la nuit et plus que très probable le jour.

La température effective de la Lune serait de -3°C. Qu’est-ce que cela signifie ?

La notion de température effective a été introduite dans la climatologie. De quoi s’agit-il ?
Voici la définition qui en est généralement donnée :

Température effective radiative :

1. Un concept théorique

On calcule une température théorique, T_eff, pour une planète “idéale” :

• pas d’atmosphère ;
• surface uniforme qui se comporte comme un corps noir (tout le solaire absorbé, tout ré-émis en IR) ;
• aucun stockage de chaleur ni inertie jour/nuit.

On pose simplement :
puissance solaire absorbée = puissance infrarouge émise vers l’espace.

D’où la formule : σ T_eff⁴ = (1 − A) S₀ / 4.
Pour la Terre : T_eff ≈ 255 K (-18 °C).

2. Ce n’est pas la température “au sol”

• La loi σ T⁴ est non linéaire : la moyenne du flux n’est pas le flux d’une température moyenne.
• La vraie Terre est hétérogène (océans, continents, pôles, déserts) et tourne ; les écarts locaux sont importants.
• Avec une atmosphère et des nuages, l’approximation “corps noir sans inertie” devient insuffisante : vapeur d’eau, convection et nuages redistribuent et stockent l’énergie.

Au lieu de dire :

« Sans atmosphère, la Terre aurait une température moyenne de −18 °C. »

il vaudrait mieux préciser :

« Sans atmosphère et si elle se comportait comme un corps noir uniforme, la température radiative effective de la Terre serait d’environ 255 K (−18 °C) ; c’est la température qu’il faut pour que la planète émette exactement l’énergie solaire qu’elle absorbe. »

La température effective représente donc une température moyenne sous l’hypothèse que l’irradiance soit uniforme, que la surface soit uniforme, qu’il n’y ait pas d’atmosphère et pas d’inertie. Sans l’hypothèse d’une irradiance uniforme, nous n’avons pas le droit, c’est d’ailleurs dit plus bas, d’appliquer la loi de Stefan-Boltzmann.

Dans le cas de la Lune, en prenant un albédo de 11 %, nous trouvons 270 K = -3°C. Mais sous un ensemble d’hypothèses qui est faux pour le rayonnement entrant et faux aussi pour le rayonnement sortant, pour deux raisons : l’irradiance sur la Lune est très loin d’être uniforme, aussi bien du côté entrant que du côté sortant. Il y a par ailleurs une inertie qui est très loin d’être négligeable, même sur la Lune.

Or, en sciences, lorsqu’une hypothèse est fausse dans un raisonnement, celui-ci ne vaut rien. Donc affirmer que la température effective de la Lune est de -3°C ne veut rien dire de concret pour la Lune. Ce concept théorique – Il est toujours possible d’inventer toutes sortes de concepts théoriques, encore faut-il justifier leurs applications pratiques – n’a aucun intérêt concret en ce qui concerne la Lune.

Celle-ci a une température moyenne de l’ordre de -75°C, sans aucun rapport avec sa température effective. L’intérêt profond de ce concept m’échappe donc totalement dans le cas de la Lune.

Dans le cas de la Terre, la situation est un peu différente : l’hypothèse d’une irradiance uniforme est juste pour le rayonnement sortant et fausse pour le rayonnement entrant. Par contre il y a une atmosphère et le sol constitué à 70% d’océan possède une inertie considérable.

En considérant le rayonnement sortant du système Terre-Atmosphère, on peut éviter les deux dernières objections. Le système Terre-Atmosphère n’est pas entouré d’une deuxième atmosphère et peut être considéré comme un corps noir dans la mesure où son échange thermique avec le cosmos ne peut se faire que par rayonnement. L’inertie de l’océan concerne le sol et non pas le système Terre-Atmosphère. Il est donc possible de tirer comme conclusion pour le rayonnement sortant de ce système qu’il est bien un rayonnement à -18°C (température effective calculée pour la « Terre », en réalité pour le système Terre-Atmosphère et pour le seul rayonnement sortant).

Cela signifie que l’Atmosphère ( c’est elle qui rayonne vers l’espace ) est à -18°C de température moyenne. Ce résultat est plus que plausible puisque la température de l’Atmosphère varie de 15°C en moyenne tout en bas à -60°C tout en haut.

Mais ce résultat n’a aucun rapport avec la température au sol et n’a pas à être rapproché de cette température au sol, pour quelle raison le ferait-on ? Au sol, toutes les hypothèses sont fausses ! La température au sol, ce n’est pas, répétons-le, la température moyenne de l’atmosphère, mais sa température maximum.

Par conséquent, comme les hypothèses sont fausses pour le rayonnement entrant, qui est très loin d’être uniforme, nous ne pouvons rien tirer comme conclusion du concept de température effective au sujet du rayonnement entrant.

S’il fait 15°C en bas de l’atmosphère, ce n’est pas à cause des gaz à effet de serre dont l’introduction ne rime à rien, mais à cause d’une part de l’éclairage du soleil le jour et d’autre part de la pression atmosphérique de l’atmosphère qui met en jeu le poids de tous les gaz de l’atmosphère, couplée notamment la nuit avec l’inertie de l’océan et les circulations de chaleur induites par les courants atmosphériques et océaniques. Les gaz à effet de serre, dont le rayonnement vers le bas ne peut pas atteindre le sol ( il est absorbé avant ) ne sont pour rien du tout dans cette affaire.

Conclusion :

La notion de température effective n’apporte qu’une seule chose de concrète concernant la Terre et rien du tout de concret concernant la Lune.

Ce qu’elle apporte de concret est très clair : Le système Terre-Atmosphère et non pas le sol peut être considéré comme un corps noir émettant dans l’espace un rayonnement à 255 K ou -18°C. Cette dernière température est la température moyenne de l’atmosphère. En aucun cas elle ne représente ni la température au sol réelle, ni non plus la température « qu’aurait le sol s’il n’y avait pas de gaz à effet de serre ». L’exemple de la Lune montre que sans atmosphère et sans gaz à effet de serre, (donc sans océan non plus puisque c’est l’océan qui met des gaz à effet de serre dans l’atmosphère), avec l’inertie propre à la Lune, le sol serait, en supposant de conserver le même albédo que celui de la Lune, ce qui est plausible, à une température moyenne de -75°C et non pas de -18°C. »

Question 3 : Comment les gaz à effet de serre peuvent-ils émettre davantage en direction du sol qu’en direction du cosmos ?

L’hypothèse sur laquelle se base la théorie de l’existence d’un effet de serre est la suivante :
les gaz à effet de serre réémettraient vers le sol un « rétro-rayonnement », en retour du rayonnement infrarouge émis par ce sol. Il est supposé une sorte de ping-pong entre le sol et l’atmosphère, ou plus exactement le sol et les gaz à effet de serre contenus dans l’atmosphère.

Voici un exemple d’explication de ce genre ( source : site ASP, assistance scolaire ) :

Le bilan radiatif du système Terre

On cherche à effectuer un bilan thermique du système Terre afin d’estimer sa température moyenne, en se basant sur le rayonnement qu’elle reçoit du Soleil. Pour cela, on fait deux hypothèses.

Tout d’abord, on considère la planète prise dans son ensemble dans un état stationnaire : la puissance surfacique thermique émise par la Terre correspond à la puissance surfacique thermique moyenne reçue par rayonnement solaire, qui correspond à 𝑃𝑠≈235 W/m².

Ensuite, on suppose que la Terre est un corps noir, c’est-à-dire qu’elle absorbe parfaitement toute la lumière reçue par le Soleil. Cette hypothèse nous permet d’appliquer la loi de Stefan-Boltzmann, qui relie la température de la planète à la puissance qu’elle émet par rayonnement lumineux (infrarouge pour la Terre) :
Ps = σ × T⁴, où 𝜎≈5,67/10⁸ W/m²K⁴ est la constante de Stefan-Boltzmann.

On obtient alors 𝑇 ≈ 254 K ≈ −19°C, en prenant la racine quatrième de P_s/σ .

On sait, même sans faire de mesures précises, que la température moyenne sur Terre est plutôt proche de 15°C que de −19°C, en réalité.

Deux éléments peuvent expliquer l’écart observé :
• une partie du rayonnement solaire n’est en fait pas absorbé par la Terre, c’est ce que l’on appelle l’albédo ;
• l’atmosphère, non prise en compte dans le modèle, joue un rôle important de réflexion et de transmission des flux thermiques, contribuant ainsi à une élévation de la température de la planète. C’est l’effet de serre.

Une remarque anecdotique s’impose, mais ne souligne peut-être qu’une faute d’inattention sans lendemain. Nous ne voyons pas clairement à quoi correspond la valeur attribuée à P_S dans ce document. La valeur du rayonnement solaire au zénith est de 1367 W/m². Puis, en pratiquant l’extraordinaire division par 4 destinée à « tenir compte » de la surface totale de la terre, passe à une valeur moyenne par m² de 1367/4 = 342 W/m² en arrondissant. Si l’albédo de 30% est pris en compte, nous trouvons 0.7 x 342= 240 W/m² . L’albédo est donc déjà pris en compte dans ce calcul. Il n’a par conséquent pas à entrer une seconde fois dans l’explication de la différence entre -19°C et 15°C, comme le suggère la fin du document.

Rappelons que beaucoup plus grave est le fait de pratiquer cette distribution afin d’obtenir une puissance moyenne. La valeur de la puissance moyenne est exacte, mais la valeur de la température moyenne trouvée est fausse pour ce qui concerne le sol. On n’applique pas la loi de Stefan-Boltzmann, qui n’est pas une loi linéaire, à une moyenne. Ceci a été expliqué à la page « L’erreur principale ». Dire que « ceci nous permet d’appliquer la loi de Stefan-Boltzmann » est donc faux. Non cela ne permet pas une telle chose, qui n’est rien d’autre qu’une hérésie physique et mathématique. Examinons en outre la valeur scientifique du dernier paragraphe de ce document :

• l’atmosphère, non prise en compte dans le modèle, joue un rôle important de réflexion et de transmission des flux thermiques, contribuant ainsi à une élévation de la température de la planète. C’est l’effet de serre. »

Certaines « explications » de l’effet de serre nous disent que l’eau et le dioxyde de carbone, lorsqu’ils ont absorbé le rayonnement infrarouge venant du sol, rayonneraient alors dans toutes les directions. Ces explications se poursuivent en nous indiquant qu’il y a autant de rayonnement qui se dirige vers le cosmos que de rayonnement retournant vers la Terre. Dans le même temps, le « bilan radiatif » qui est fait donne 240W/m² comme chiffre du rayonnement vers l’espace et 330W/m² comme valeur du rétro-rayonnement, justifiant ainsi dans certains cas la raison pour laquelle il serait « évident » qu’il y a un effet de serre. La différence entre ce 330 W/m² retournant vers le bas et ce 240 W/m² en sortie étant la cause du réchauffement du sol par l’effet de serre. Cela signifie dans ce cas que les gaz effet de serre rayonnent 90 W/m² de plus vers la terre que vers le cosmos. Nous posons alors la question : quelle est la source de chaleur qui crée ces 90 W/m² en plus?

Tout cela ne tient pas debout, c’est en tout cas notre conclusion personnelle. Il n’est pas possible de dire en même temps que le rayonnement des gaz à effet de serre est égal vers le haut et vers le bas et chiffrer à 330 W/m² le rayonnement vers le bas et à seulement 240 W/m² le rayonnement vers le haut. Dès lors, ils ne sont plus égaux…

Il n’est pas possible non plus d’affirmer en même temps que cette différence correspond à l’effet de serre et qu’elle ne consiste pas en un apport de chaleur supplémentaire qui serait créé ( par miracle ? ) par la présence des gaz à effet de serre. 240 W/m² est l’irradiance sortante moyenne nécessaire pour que la Terre soit en équilibre radiatif. Si les gaz à effet de serre émettent 330 W/m² vers le sol dans ces conditions, c’est donc qu’ils doivent constituer intrinsèquement une source de chaleur capable d’irradier en plus 90 W/m². Il est évident que cette perspective est absurde.

Commentons pour finir la phrase rappelée ci-dessous :

On sait, même sans faire de mesures précises, que la température moyenne sur Terre est plutôt proche de 15°C que de −19°C, en réalité.

Il est question juste avant de dire ceci : Cette hypothèse nous permet d’appliquer la loi de Stefan-Boltzmann, qui relie la température de la planète à la puissance qu’elle émet par rayonnement lumineux (infrarouge pour la Terre) :

Or, qui émet vers le cosmos ? Ce n’est pas le sol en lui-même. C’est la système Terre-atmosphère tout entier. La photo ci-dessous montre que ce système émet à partir d’une sphère située en haut de l’atmosphère, de façon pratiquement uniforme. C’est ce système et non pas le sol qui est à une température moyenne de -19°C. Ce chiffre n’a donc pas à être comparé aux 15°C qui règnent au sol. Faire une telle comparaison, ce n’est donc rien d’autre qu’une faute scientifique, qui s’apparente de près à de la désinformation. Comme nous ne sommes pas complotistes, nous dirons simplement qu’il n’y a probablement pas de volonté, derrière cette erreur évidente, de tromper le grand public. C’est simplement une erreur, qui est grave sur le plan scientifique. Nous pensons que les climatologues s’honoreraient de le reconnaitre honnêtement.

Question 2 : Un radiateur à infrarouge chauffe une pièce. Il reçoit en retour un rayonnement. D’où vient ce rayonnement ? Des murs et du plafond ou de l’air de la pièce ?

Essai de réponse :

Le principe du chauffage par radiateur à infrarouge est décrit ainsi sur les sites vendeurs. Voici un exemple sur le site tenu par Thermor :

« Un radiateur radiant se distingue des autres technologies de chauffage par sa manière de chauffer son environnement.

Le chauffage radiant c’est le processus de la chaleur se déplaçant par rayonnement sous forme d’ondes plutôt que de particules comme la convection par exemple. L’énergie peut être transférée d’un corps à haute température à un corps à basse température sans qu’ils aient à être en contact les uns avec les autres. Il s’agit de la même méthode de transfert de chaleur que les rayons du soleil qui vous réchauffent : les rayons infrarouges. C’est aussi pourquoi vous pouvez sentir la chaleur d’un feu lorsque vous êtes à une distance de celui-ci et sans le toucher.

Les systèmes de chauffage radiant chauffent des objets solides, y compris des humains, plutôt que d’utiliser l’air qui nous entoure pour nous réchauffer. Ils sont plus efficaces pour chauffer les surfaces ternes, mates ou rugueuses que les surfaces brillantes, car les surfaces brillantes réfléchiraient les ondes de rayonnement. Lorsque l’objet solide a été chauffé par chauffage radiant, il « dégage sa chaleur vers l’air environnant ». Les radiateurs rayonnants n’ont donc pas besoin d’être allumés aussi longtemps que les appareils de chauffage conventionnels et sont moins affectés par les courants d’air froids. »

Il est donc assez clair que la réponse à la question posée n’est donc pas : c’est l’air de la pièce qui renvoie un rayonnement vers le radiateur. Ceci n’est pas pour étonner l’auteur de ces lignes, qui sait fort bien qu’un gaz ne peut pas en thermodynamique, être assimilé à un corps noir. S’il est exact que deux corps solides comme par exemple deux mains approchées l’une de l’autre peuvent être considérées sans faire d’erreur significative comme deux corps noirs, ceci est faux lorsque l’on met en présence une surface solide ou liquide rayonnante avec un gaz. Les deux mains rayonnent en effet toutes deux à leur température de 37°C et s’envoient mutuellement un rayonnement égal à celui qu’elles ont reçu. Les deux mains ne se chaufferont pas puisqu’elles sont à la même température. Par contre, une main placée près d’un objet solide froid va, en envoyant un rayonnement vers cet objet, le réchauffer, jusqu’à ce qu’ils soient à la même température. La situation ainsi créée est une situation d’équilibre et elle ne changera plus ensuite parce que, l’objet solide étant désormais à la même température que la main, il renverra vers elle un rayonnement désormais égal à celui qu’il reçoit.

Le problème est qu’avec les gaz, cela ne se passe pas de cette manière. Un gaz dit à effet de serre comme le sont la vapeur d’eau et le CO₂ ne peuvent pas être assimilés à des murs ou à des plafonds pouvant renvoyer un rayonnement vers leur source de chaleur. Ce ne sont pas des corps noirs. C’est pourtant ce qu’affirment les tenants de l’existence d’un effet de serre. Eh bien, il faut savoir que ceci est tout à fait faux. D’où vient la croyance, car c’en est une, que les gaz à effet de serre rayonneraient du haut de l’atmosphère vers le sol ? Il faut reconnaitre que la réponse n’est pas évidente, parce que les instruments de mesure cherchant à mesurer ce soi-disant rayonnement « renvoyé » par les gaz à effet de serre détectent effectivement un rayonnement infrarouge venant du haut et parvenant jusqu’au sol. Les mesures en question l’évaluent même à la valeur de 330 W/m². A notre avis la question qui ne semble jamais être posée est celle-ci : ce rayonnement infrarouge qui vient d’en haut de l’atmosphère vient-il de ce que l’on appelle un rétro-rayonnement, autrement dit à la suite d’une sorte de jeu de ping-pong entre le sol terrestre et les gaz à effet de serre, ce qui est la seule hypothèse retenue, où vient-il beaucoup plus simplement et directement du Soleil lui-même ? La « question pour réfléchir suivante » est entièrement consacrée à l’étude de cette question.  Nous apportons plus bas simplement des informations de base sur les questions de spectroscopie.

Il n’est en effet pas dans notre propos ici de faire un cours de spectroscopie très complet et très technique sur ces questions. Par contre, il nous parait normal et légitime d’en exposer les conclusions et de dire honnêtement l’état des connaissances sur la question.

Voici tout d’abord à quoi ressemble le spectre d’un corps noir, comme l’est sans faire d’erreur significative, le spectre de la lumière solaire :

Un spectre de corps noir ou « assimilé » de façon raisonnable à un corps noir est tout d’abord un spectre continu. Il couvre toute une très large gamme de longueurs d’onde. Dans le cas du Soleil, cette gamme va des rayons ultra-violets les plus énergétiques aux rayons infrarouge et jusqu’aux très longues ondes radio, en passant par le rayonnement dit visible illustré par les couleurs de l’arc-en-ciel dans l’image ci-dessus (source Wikipedia). Ce spectre présente, comme tous les spectres de corps noir, un maximum qui dépend de la température du corps noir, ici de celle du Soleil.

Le « spectre » d’un gaz susceptible d’absorber du rayonnement n’est pas continu. Il est formé au contraire de raies bien distinctes les unes des autres. Voici les spectres de la vapeur d’eau, illustrés sur le site de l’institut français de l’éducation :

L’étude du rayonnement dans les gaz est l’objet de ce que l’on appelle la spectroscopie, science née avec Newton et ses travaux sur la lumière. Voici un document résumant les connaissances acquises à ce sujet (source : Faculté des sciences de Rabat) :

Que conclure de tout ceci en pratique ? Ceci est exposé sur le site du professeur Geuskens.

https://www.science-climat-energie.be/author/geuskensulb-ac-be/

En simplifiant les choses, l’idée d’un rétro-rayonnement des gaz à effet de serre vers le sol se heurte à trois objections difficilement réfutables, que nous exposons ci-dessous :

La première est que les gaz à effet de serre ne peuvent rayonner qu’à des pressions ou des températures bien plus faibles que celles qu’ils trouvent en bas de l’atmosphère. En bas, la quasi totalité du rayonnement infrarouge du sol vers l’atmosphère est transformé en énergie cinétique, agitant les molécules. Ceci est la définition même de la chaleur au niveau corpusculaire : la chaleur mesure le degré d’agitation des molécules. Il en résulte que les gaz à effet de serre chauffent eux-mêmes et chauffent par suite leur environnement, c’est-à-dire les autres molécules de l’air, qui s’agitent et se heurtent, selon un mécanisme appelé convection. La convection entraine la montée de la chaleur dans l’atmosphère et comme il n’y a ni mur ni plafond au dessus, il n’y a statistiquement quasiment pas de rayonnement, en tout cas pas de rayonnement mesurable, dans toute la zone, en gros la troposphère, où cette convection continue son effet. L’air se refroidit et la pression diminue avec l’altitude. Arrivée aux alentours de l’isotherme -18°C, la pression est suffisamment faible pour qu’il soit possible aux gaz à effet de serre ( essentiellement à la vapeur d’eau) de rayonner. Il n’y a donc aucun ou très peu statistiquement de rayonnement des gaz à effet de serre dans toute la zone dite convective.

La seconde est qu’il n’y a aucune raison sérieuse d’admettre que le rayonnement émis vers l’isotherme -18°C qui redescend en partie vers le bas puisse valoir autant que le rayonnement infrarouge du sol. Il se partage statistiquement en deux moitiés, l’une vers le cosmos et l’autre vers le sol. Ce n’est pas ce que montrent les « bilans radiatifs » exposés par les tenants de ces théories.

La troisième est qu’il n’y a aucune raison sérieuse non plus de penser que ce rayonnement vers le bas ne soit pas à son tour absorbé par les gaz à effet de serre situés plus bas que l’altitude d’émission. Nous ne voyons pas au nom de quoi il serait permis de supposer que le rayonnement du sol soit absorbé parce qu’il circule dans le sens de la montée et le rétro-rayonnement, bien moins intense, qui serait renvoyé vers le bas ne serait pas absorbé parce qu’il circule quand à lui dans le sens de la descente.

Tout ceci montre clairement l’extrême fragilité de la théorie de l’effet de serre.

Question 1 : Comment expliquer la température à la surface du soleil ? Un bilan radiatif est-il utile dans ce cas ?

Essai de réponse :

La température solaire s’explique par l’existence au centre de notre étoile de réactions thermonucléaires. L’origine de ces réactions est bien identifiée. Il s’agit de la force de gravitation. La pression exercée sur la matière qui se trouve au centre du Soleil est tellement grande que les scientifiques parlent d’un « effondrement » de la matière sur elle-même. C’est cet effondrement qui explique le déclenchement des réactions thermonucléaires au centre de notre étoile. L’énergie en jeu dans ce processus est colossale et n’est due à rien d’autre qu’à la force gravitationnelle.

Les rayonnements qui parviennent à la surface du Soleil depuis le cosmos sont dans ce contexte tout à fait anecdotiques. Il y a le rayonnement du fond du ciel, appelé rayonnement à 3K ( tout rayonnement est associé à une température ), plus que négligeable. Il y a probablement un rayonnement très marginal du système planétaire vers le Soleil et aussi un rayonnement encore plus marginal des étoiles les plus voisines. Sans doute quelques traces de rayonnement cosmique d’origine non identifiée. Toujours est-il que ces rayonnements sont sans influence sur la température qui règne à la surface du Soleil, et ce d’autant moins qu’un rayonnement ne peut « chauffer » une surface atteinte que si sa température associée dépasse celle de cette surface.

Qu’en tirer dans nos réflexions sur le climat ?

De ces constatations nous pouvons tirer l’enseignement suivant : faire un bilan seulement radiatif d’un astre aux fins de déterminer sa température de surface est une entreprise qui sera vouée à l’échec dans la plupart des cas. L’entreprise possède en effet un défaut majeur, qui est celui d’ignorer que l’une des causes susceptibles d’influencer la température qui règne à la surface d’un astre est, lorsque cet astre est muni d’une atmosphère, la pression qu’exerce cette atmosphère sur les gaz situés près du sol. Ainsi, faire un bilan seulement radiatif n’a de sens que si l’astre n’est pas entouré d’une atmosphère.

Un bilan radiatif sur la Lune peut éventuellement être fait, puisqu’il n’y a pas d’atmosphère.

Un bilan radiatif sur la Terre peut toujours être fait, mais ne donnera que des résultats partiels ne permettant que de se rendre compte de l’action du seul Soleil. Les résultats ne correspondront pas aux températures réelles puisque la gravitation n’aura pas été prise en compte. Tirer des conclusions sur l’existence d’un effet de serre à partir de résultats tronqués est tout simplement irresponsable.

Il est entendu, pratiquement dans le monde entier, que le réchauffement climatique observé actuellement, réchauffement qui n’est pas contesté par l’auteur de ce site, aurait une cause anthropique, c’est-à-dire qu’il serait dû aux activités humaines et notamment aux émissions de gaz à effet de serre.

L’auteur est en complet désaccord avec cette affirmation, pour des raisons physiques et mathématiques.

Dans la réalité, l’invention d’un effet de serre naturel est tout simplement le résultat de calculs et surtout de raisonnements visiblement faux. Ceci est expliqué et détaillé dans les articles et les pages parus ou à paraître prochainement sur ce site.

L’auteur, Yves Courtieu, mathématicien indépendant.

La dent d’or (Fontenelle):

« Il serait difficile de rendre raison des histoires et des oracles que nous avons rapportés, sans avoir recours aux démons, mais aussi tout cela est-il bien vrai ? Assurons-nous bien du fait, avant de nous inquiéter de la cause. Il est vrai que cette méthode est bien lente pour la plupart des gens, qui courent naturellement à la cause, et passent par-dessus la vérité du fait ; mais enfin nous éviterons le ridicule d’avoir trouvé la cause de ce qui n’est point. »

« Ce malheur arriva si plaisamment sur la fin du siècle passé à quelques savants d’Allemagne, que je ne puis m’empêcher d’en parler ici. »

« En 1593, le bruit courut que les dents étant tombées à un enfant de Silésie, âgé de sept ans, il lui en était venu une d’or, à la place d’une de ses grosses dents. Horstius, professeur en médecine dans l’université de Helmstad, écrivit en 1595 l’histoire de cette dent, et prétendit qu’elle était en partie naturelle, en partie miraculeuse, et qu’elle avait été envoyée de Dieu à cet enfant pour consoler les chrétiens affligés par les Turcs. Figurez-vous quelle consolation, et quel rapport de cette dent aux chrétiens ni aux Turcs. En la même année, afin que cette dent d’or ne manquât pas d’historiens, Rullandus en écrit encore l’histoire. Deux ans après, Ingolstetetus, autre savant, écrit contre le sentiment que Rullandus avait de la dent d’or, et Rullandus fait aussitôt une belle et docte réplique. Un autre grand homme nommé Libavius ramasse tout ce qui avait été dit de la dent, et y ajoute son sentiment particulier. Il ne manquait autre chose à tant de beaux ouvrages, sinon qu’il fût vrai que la dent était d’or. Quand un orfèvre l’eut examinée, il se trouva que c’était une feuille d’or appliquée avec beaucoup d’adresse ; mais on commença par faire des livres, et puis on consulta l’orfèvre. »

« Rien n’est plus normal que d’en faire autant sur toutes sortes de matières. Je ne suis pas si convaincu de notre ignorance par les choses qui sont, et dont la raison nous est inconnue, que par celles qui ne sont point, et dont nous trouvons la raison. Cela veut dire que non seulement nous n’avons pas les principes qui mènent au vrai, mais que nous en avons d’autres qui s’accommodent très bien avec le faux. »

— Fontenelle, Histoire des oracles, IV.

Utilisez les commentaires de cet article si vous souhaitez réagir au contenu de l’article que j’ai écrit, publié sur la page « Article réfutant l’effet de serre ».
Je suppose que vous l’avez lu très attentivement, comme demandé.