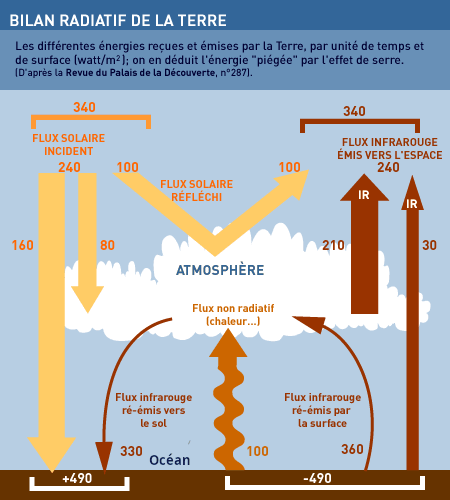
Le flux arrivant en haut de l’atmosphère est donc chiffré à 340 W/m² … On notera qu’il n’est fait aucune différence entre le pôle et l’équateur… L’un comme l’autre reçoivent soi-disant 340 W/m² .

On notera aussi qu’il s’agit d’une sphère éclairée de la même façon de jour comme de nuit… Or, la nuit, il n’arrive aucun rayonnement, ou, si vous préférez et qui ne change rien à l’absurdité de ces chiffres, le rayonnement est nul la nuit…

On notera enfin que la valeur de la constante solaire, qui correspond à la puissance du rayonnement qui arrive au point situé au zénith, est de 1367 W/m² et non pas de 340 W/m² .

Comment peut-on avancer sérieusement des chiffres semblables à ceux de ce schéma ? Cela me parait inconcevable !

D’où vient donc le chiffre de 340 W/m² ? Il s’agit de la distribution sur l’ensemble de la sphère terrestre du rayonnement incident. Le total du rayonnement incident est calculé ( très correctement d’ailleurs, disons-le tout de même ici ) à partir du disque intercepté par le rayonnement solaire. Ce disque a pour surface πR², où R est le rayon de la Terre.  Le total obtenu, qui vaut 1367 πR², exprimé en watts, est ensuite distribué sur l’ensemble de la surface terrestre. Or, la surface totale de la sphère est 4πR², soit quatre fois plus grande que le disque. Pour conserver le même total d’énergie, la puissance du rayonnement « moyen » par m² doit donc être divisée par 4, ce qui donne environ 340 W/m². La moyenne ainsi obtenue est certes exacte en tant que moyenne, mais l’employer dans des calculs de température est totalement absurde ! Ce sont les relevés locaux (ou les calculs quand c’est possible) de température qui permettent de trouver la moyenne des températures et non pas des moyennes d’irradiance qui permettent de reconstituer les valeurs locales de température. Ceci est l’évidence même…

Nous allons examiner quelques arguments parmi ceux qui nous ont été servis pour justifier ces chiffres. Le lecteur sera laissé juge de ce qu’ils valent.

Argument n°1 :

L’inertie thermique considérable de l’océan donnerait le droit de faire cette approximation. Il s’agit là de l’une de ces approximations « au lance-pierre » dont peuvent parfois être friands mes confrères physiciens. Faire ce genre d’approximations est, la plupart du temps, une démarche utile et fructueuse dans leur science. Mais, ici, le seul qualificatif qui me vient à l’esprit est que cette approximation est totalement injustifiée. Elle est même inconcevable ! Pourquoi ? 

Voici une première raison : l’océan se trouve au ras du sol et non pas en haut de l’atmosphère. Dire que l’inertie thermique justifie l’approximation faite signifierait donc que l’action de l’océan se téléporte en quelque sorte, depuis le ras du sol jusqu’en haut de l’atmosphère… Comment justifier autrement qu’AVANT de rentrer dans l’atmosphère, le rayonnement solaire se répartisse tout autour de la Terre en raison de l’inertie thermique de l’océan, situé, lui, au ras du sol. Un tel argument laisse absolument sans voix quiconque réalise ce qui se dit ici ….

Et voici une seconde raison : l’inertie thermique de l’océan joue un rôle effectivement très important sur la température qui règne au sol. Mais, dire que l’inertie thermique justifie l’approximation qui a été faite, c’est transformer l’action de l’inertie thermique, qui porte sur la température au sol, en une action modifiant le rayonnement solaire incident. C’est donc confondre la température qui règne au sol avec la puissance du rayonnement incident, qui arrive en haut de l’atmosphère. Il est impossible de souscrire à de telles considérations…

Argument n°2 :

Je faisais remarquer à plusieurs de mes interlocuteurs que l’article de Hurley & al. (voir la page « Fausseté des calculs » ) ne faisait pas de pareille moyenne pour modéliser la température sur la Lune et que, de plus, utiliser une telle moyenne conduisait à trouver une température moyenne sur la Lune de -6°C, au lieu des -73°C mesurés par le satellite Lunar Orbiter. 

La réponse obtenue fut dans chaque cas qu’il n’était pas possible d’appliquer au cas de la Terre le raisonnement employé pour la Lune. Pour appuyer leur propos, il était question de la différence de durée de la rotation de ces deux astres, de la présence de courants atmosphériques ou de nuages sur la Terre alors que la Lune n’avait aucune atmosphère. Nous sommes de nouveau en présence de la même erreur typique. Tous les phénomènes sont mélangés au lieu de les analyser un par un… En outre, j’aimerai que l’on m’explique la différence qu’il y a entre l’interface « haut de l’atmosphère terrestre – cosmos » et l’interface « sol lunaire – cosmos » ! Ou encore en quoi la durée de rotation de la Terre influe-t-elle le rayonnement solaire qui arrive à chaque instant en haut de l’atmosphère ? Ce doit être, probablement, un rayonnement qui tourne autour de la terre afin de pouvoir l’éclairer la nuit à chaque instant (ironie)… Encore une fois, il y a confusion entre le rayonnement solaire en haut de l’atmosphère et ce qui influe, à l’intérieur de l’atmosphère, sur la température… A moins que l’action des nuages ne se téléporte, elle aussi, dans le cosmos, avant que le rayonnement n’entre dans l’atmosphère terrestre (ironie de nouveau)…

Argument n°3 :

J’ai fait la comparaison suivante, pour illustrer l’erreur manifeste de ces raisonnements : prenons une classe de 30 élèves. Le professeur leur fait subir une épreuve. 15 sont absents et 15 sont présents. Les 15 élèves présents ont obtenu chacun la note de 14/20. Il est possible alors de calculer deux moyennes: celle des présents, qui est de 14×15/15 = 210/15 =14/20, et celle de la classe entière, qui est de (14×15+0x15)/30 = 210/30 = 7/20.

Si l’on procède de manière analogue à ce que nous avancent les calculs du GIEC, la réalité des notes obtenues est alors traduite par « tout revient à ce que chacun des 30 élèves aient obtenu la note de 7/20 »

Je me suis vu répondre que ma comparaison n’était pas pertinente, parce qu’il fallait considérer non pas que les élèves étaient absents, mais qu’ils avaient tous rendus copie blanche, et donc avaient bien obtenu la note de zéro. Mais en quoi cette réponse change-t-elle la réalité ? Dans ces conditions, peut-on dire que tout revient à ce que chaque élève ait bien eu une note de 7/20 ?

Selon moi, la réalité reste quasiment inchangée puisque les élèves ont obtenus la note de 14/20 pour quinze d’entre eux et la note de 0/20 pour quinze d’entre eux (au lieu d’être absents, ce qui est la seule différence, laquelle ne change pas grand chose à la fausseté du raisonnement tenu). 

Dans la réalité, absolument personne n’a obtenu la note de 7/20. La moyenne obtenue est exacte, mais l’employer pour reconstituer les notes des élèves est à l’envers ! Ce sont les relevés de notes réelles qui permettent de calculer la moyenne et non pas la moyenne qui permet de reconstituer les notes des élèves. C’est, là aussi, l’évidence même…

Trêve de plaisanterie !

Dans la réalité, le rayonnement entrant est variable selon la position du mètre carré de surface éclairé, en haut de l’atmosphère, bien sûr. Considérer une variable comme fixe en utilisant une moyenne pour calculer sa soi-disant valeur n’est rien d’autre qu’une erreur logique grave. Si nous appelons θ l’angle entre la normale à la sphère en un point de la face éclairée et la direction du soleil, nous obtenons un rayonnement entrant, en haut de l’atmosphère, égal en W/m², à 1367 cos θ en ce point, côté jour donc et nous obtenons un rayonnement égal à 0 en toute surface de 1 m² plongée dans la nuit.

Telle est la formule mathématique assez simple à comprendre et pourtant considérée comme fausse par mes collègues : je vous le redis, je n’en reviens pas ! 

Faire les calculs qui sont faits à partir de moyennes inutilisables dans ce contexte est pour moi de l’ordre de l’inconcevable.